Finora abbiamo trattato due principali metodologie di modellazione, la prima ha un carattere tecnico-progettuale in quanto mira ad assemblare diverse forme tridimensionali riconducibili a delle primitive (mesh, curve, superfici, etc), mentre l’altra è più artistica e passa per gli strumenti dello sculpting. Tuttavia esiste anche un terzo paradigma che è la modellazione parametrica. Una delle principali novità introdotte con le release 2.9x di Blender e poi raffinata con la serie 3.x è il sistema del Geometry Nodes tramite cui è possibile creare un’infinità di modelli, come anche intere scene sia realistiche, sia astratte, il tutto utilizzando la logica del node editor già vista in azione nelle finestre: shader editor e compositor. Questo argomento non è da considerarsi indispensabile in una guida introduttiva alla grafica 3D, ma dato che sul web ormai fioccano molti tutorial relativi a scene e modelli creati con l’ausilio dei Geometry Nodes (alcuni di enorme complessità) ho ritenuto opportuno inserire questo paragrafo nella guida.
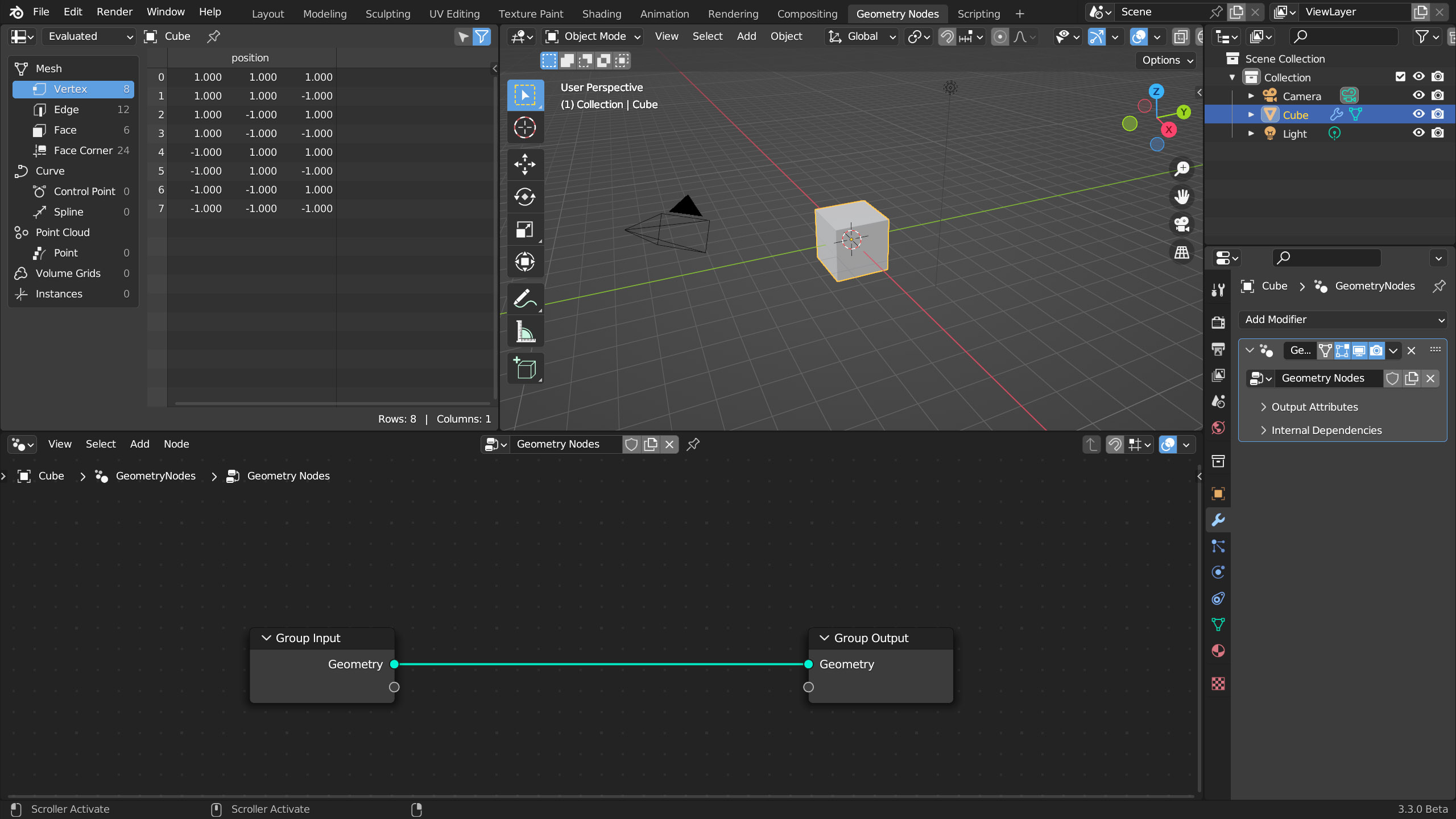
Partiamo dal workspace Geometry Nodes di Blender, costituito da tre finestre incluso ovviamente il cruciale editor a nodi. Selezioniamo una qualsiasi mesh come ad esempio il cubo di default e clicchiamo ![]() nel node editor appariranno i due nodi Group Input e Group Output visibili nell’immagine seguente
nel node editor appariranno i due nodi Group Input e Group Output visibili nell’immagine seguente
I socket di entrambi i nodi sono di colore verde acqua, il quale indica la trasmissione dell’informazione relativa alla geometria della nostra mesh. Lo scopo di qualsiasi combinazione di nodi è quello di trasformare una geometria iniziale in una differente geometria finale, cosa che potrebbe comportare la variazione significativa del numero di vertici e facce, secondo una distribuzione spaziale più o meno complessa. La geometria finale potrà essere anche una combinazione di diverse mesh, sia primitive, sia modellate in precedenza. Come già visto per altri strumenti di Blender, anche in questo caso, ma forse è meglio dire specialmente in questo caso, l’argomento è talmente vasto (e non interamente esplorato neanche dagli utenti più smaliziati) che da solo meriterebbe un libro a parte. Quindi non darò una visione completa dei nodi disponibili (oltre 100) ma mostrerò alcuni esempi tipici, anche perché molti nodi sono del tutto analoghi a quelli impiegati in altri contesti (ad esempio i nodi relativi alle operazioni sui dati numerici, dati colore e vettoriali, etc). Dunque sarà più semplice sperimentare con i geometry nodes soltanto dopo aver acquisito esperienza con la logica dello shader editor e/o del compositor, ossia argomenti trattati nei paragrafi e capitoli precedenti che hanno una maggiore priorità nella fase di apprendimento del software.
Anche nei geometry nodes troviamo dei socket gialli (dati colore), grigi (parametri numerici) e viola (dati vettoriali) più altri colori che al momento è inutile elencare. Nel workspace Geometry Nodes il pannello delle properties appare settato sul contesto Modifier, e qui capiamo che qualunque combinazione di nodi andremo a definire, essa non sarà distruttiva in quanto agirà sulla mesh come un normale modificatore. Partiamo da un banale piano e cominciamo a modificarne la geometria con il nodo Subdivide (famiglia nodi Mesh) posto tra i nodi Group Input e Group Output.
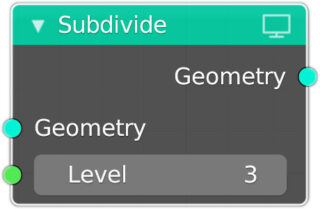
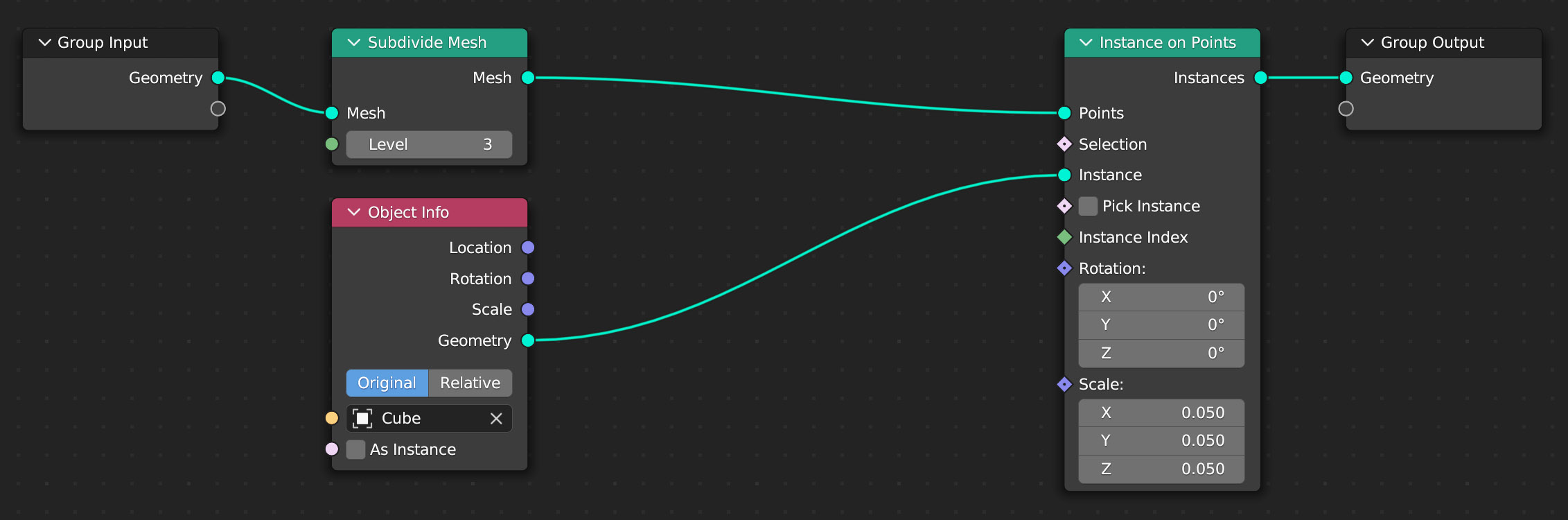
Non vedrete l’effetto di questo nodo a meno che nel contesto properties Object, pannello Viewport Display non attiviate la visualizzazione Wireframe. In tal caso potrete passare alla modalità edit e constatare che in realtà la mesh del piano resta di quattro soli vertici. Il nodo subdivide possiede un socket input di colore verde (e non grigio) per pilotare il livello di suddivisione che tuttavia è un parametro numerico di tipo intero. Ora inseriamo nella scena (non importa dove) un semplice cubo, magari rendendolo invisibile, dopodiché introduciamo due nuovi nodi Instance on Points e Object Info esattamente come nella figura in Basso.
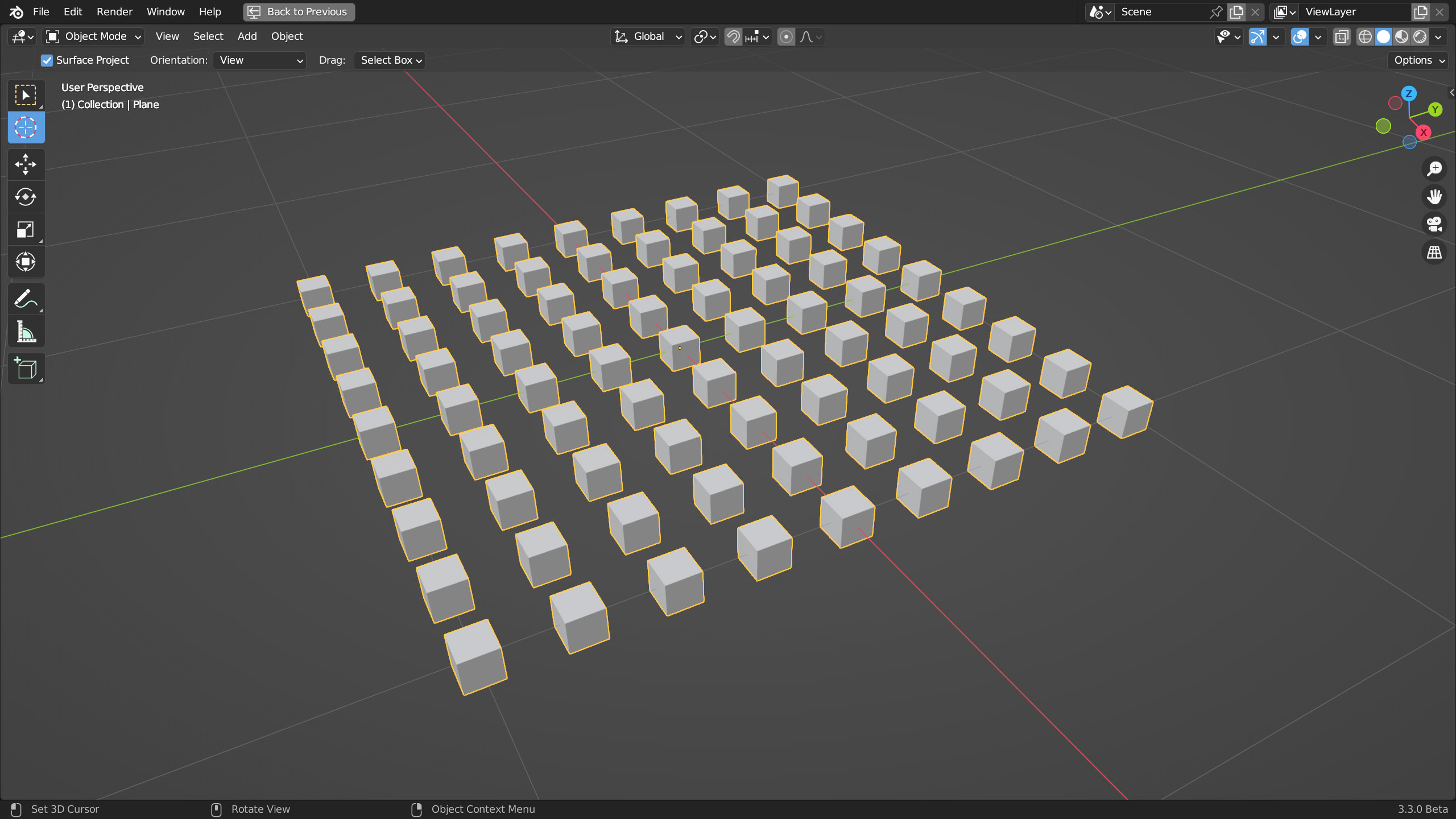
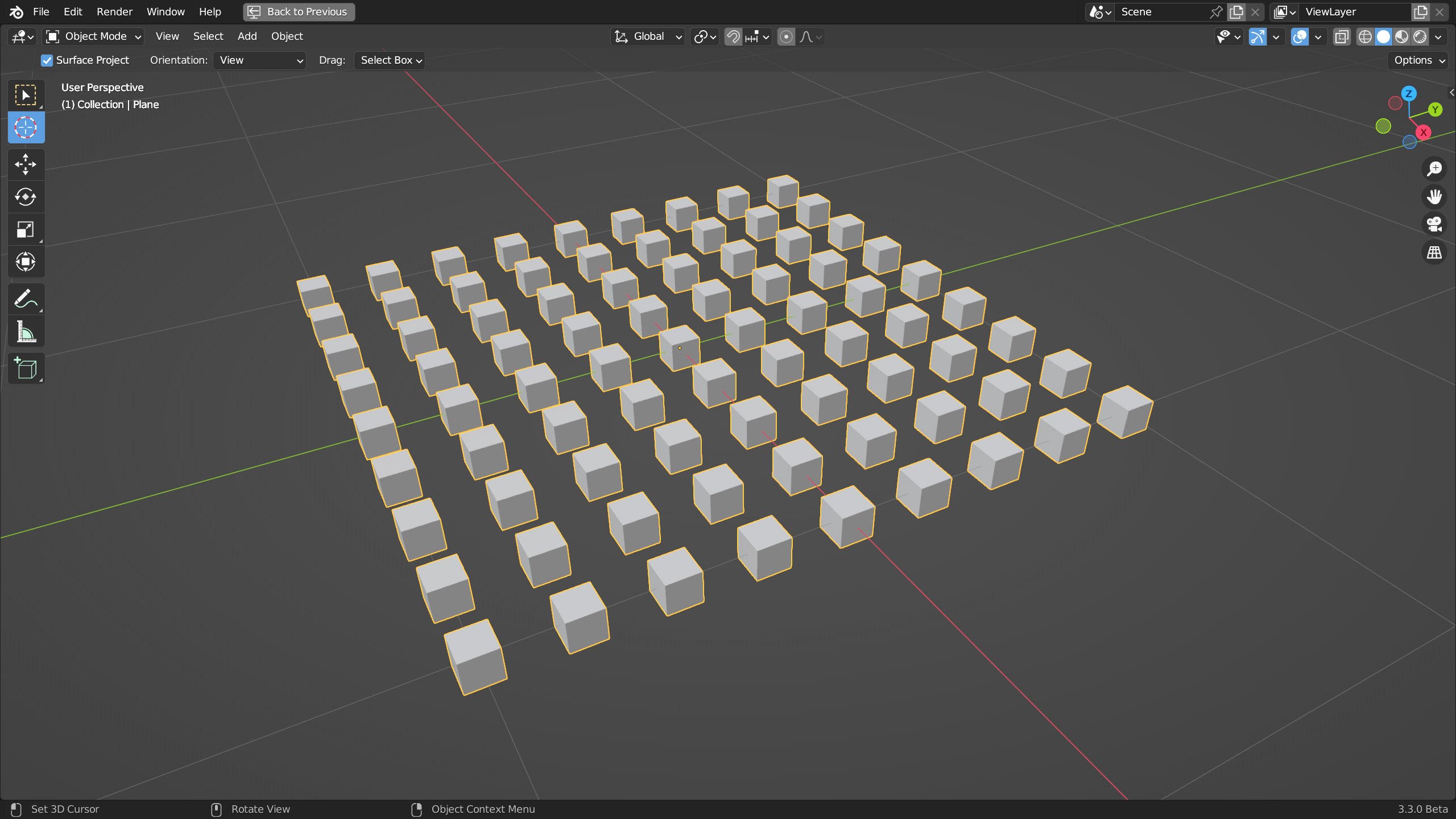
In Object Info avremo indicato il nostro cubo. Cosa succede esattamente con questa combinazione di nodi? Sappiamo che il piano è composto da quattro vertici, ossia semplicemente quattro punti nello spazio 3D. Con subdivide potremo aumentare vertiginosamente tale numero tanto che conviene fermarci a tre sole suddivisioni (81 vertici). Il nodo Istance on Points inserirà in ognuno di questi punti/vertici il cubo da noi scelto. Tuttavia le dimensioni di questo cubo potrebbero essere tali da trovarli tutti parzialmente sovrapposti, motivo per cui nel nodo Instance on Points ho impostato un fattore di scala pari 0.05 per le tre dimensioni. Il risultato è quello visibile nell’immagine seguente
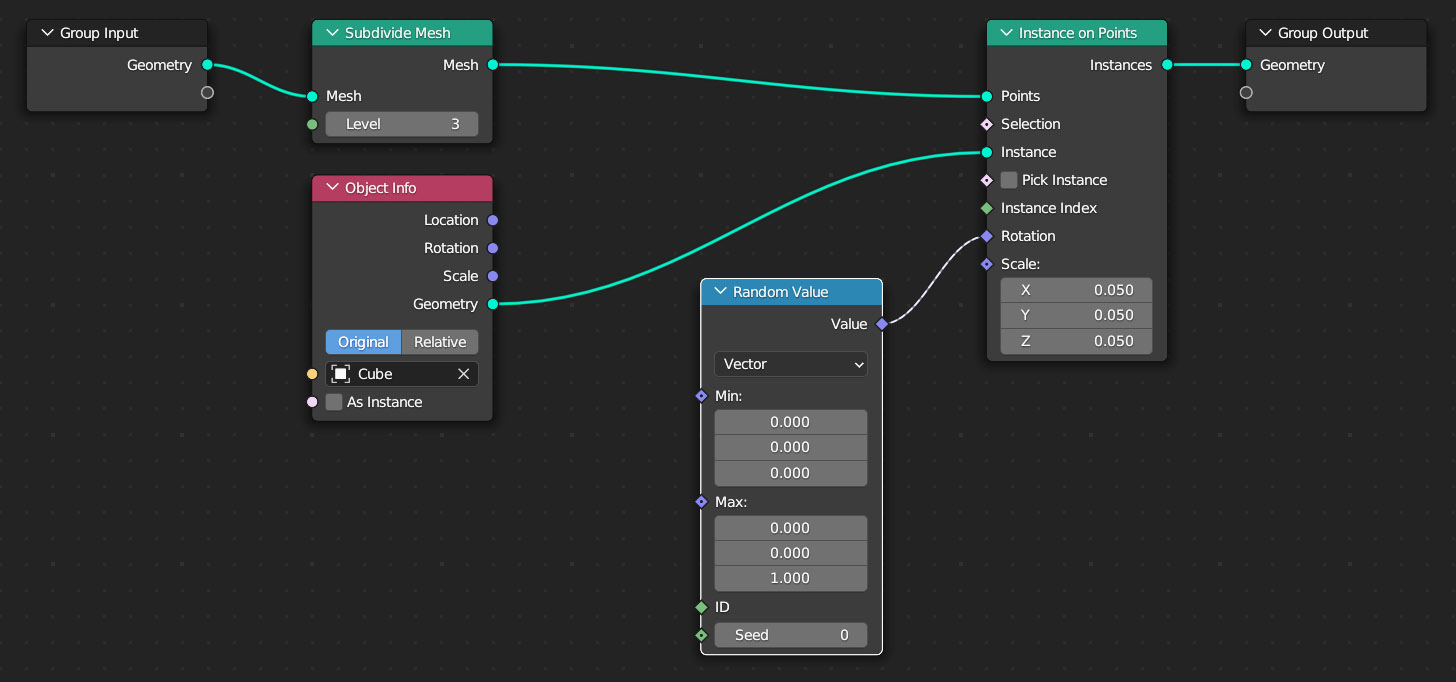
Ovviamente questa immagine non desta alcun particolare interesse essendo qualcosa che si può facilmente ottenere con il modificatore Array. Aggiungiamo allora il nodo Random Value (famiglia Utilities) in modalità Vector (vettore). Qui troveremo dei valori Min e Max di rotazione per le componenti x y e z (spazio local). Occorre fare attenzione perché tali valori non sono i consueti gradi sessadecimali, ma bensì radianti. Un radiante è pari a 57.2958°, Pi Greco (3.142) è pari a 180°. Come vedete nell’immagine ho impostato i valori minimi a 0 mentre per i valori massimi solo il terzo (corrispondente a z) è impostato a 1 radiante.
L’effetto è quello di una rotazione casuale dei cubetti intorno al proprio asse z (local) di un angolo compreso tra 0 e 1 radiante.
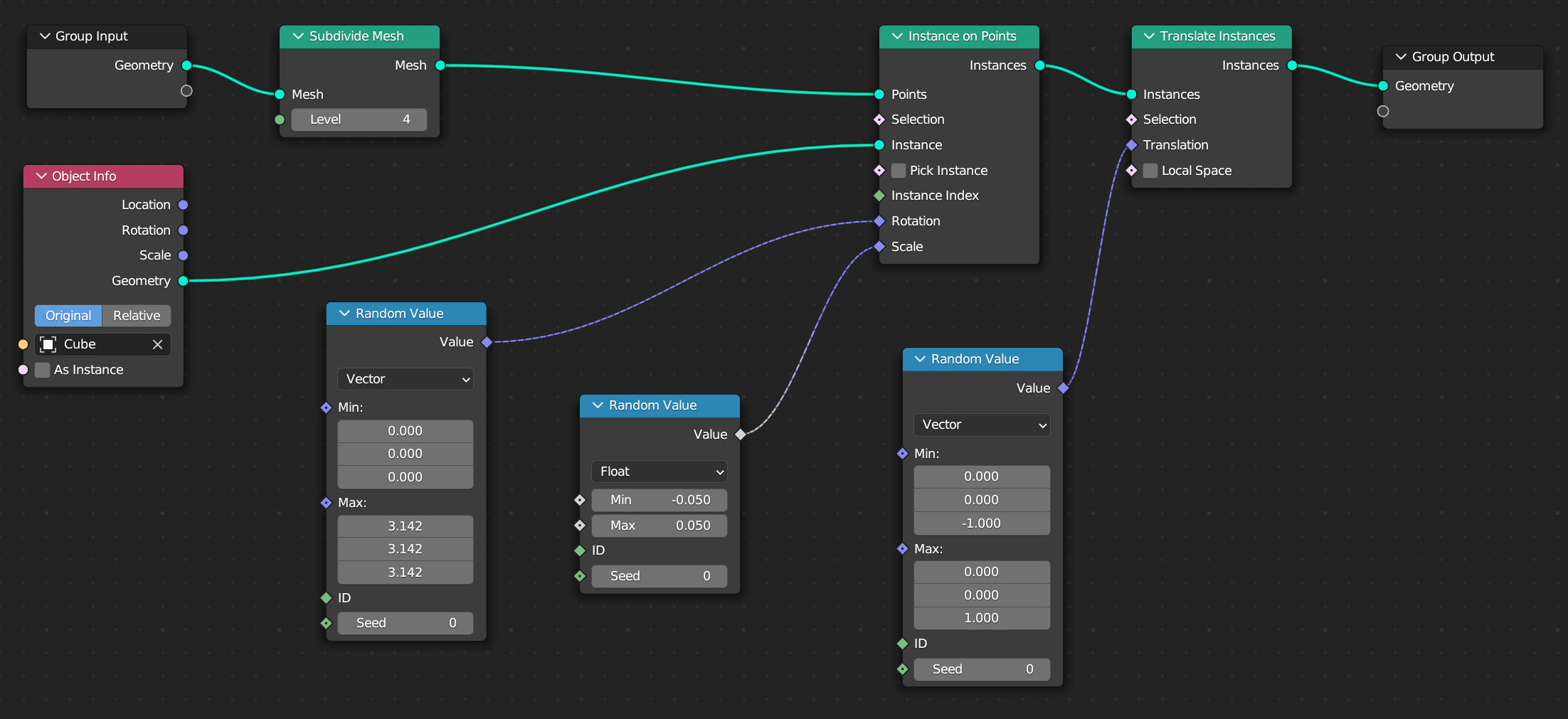
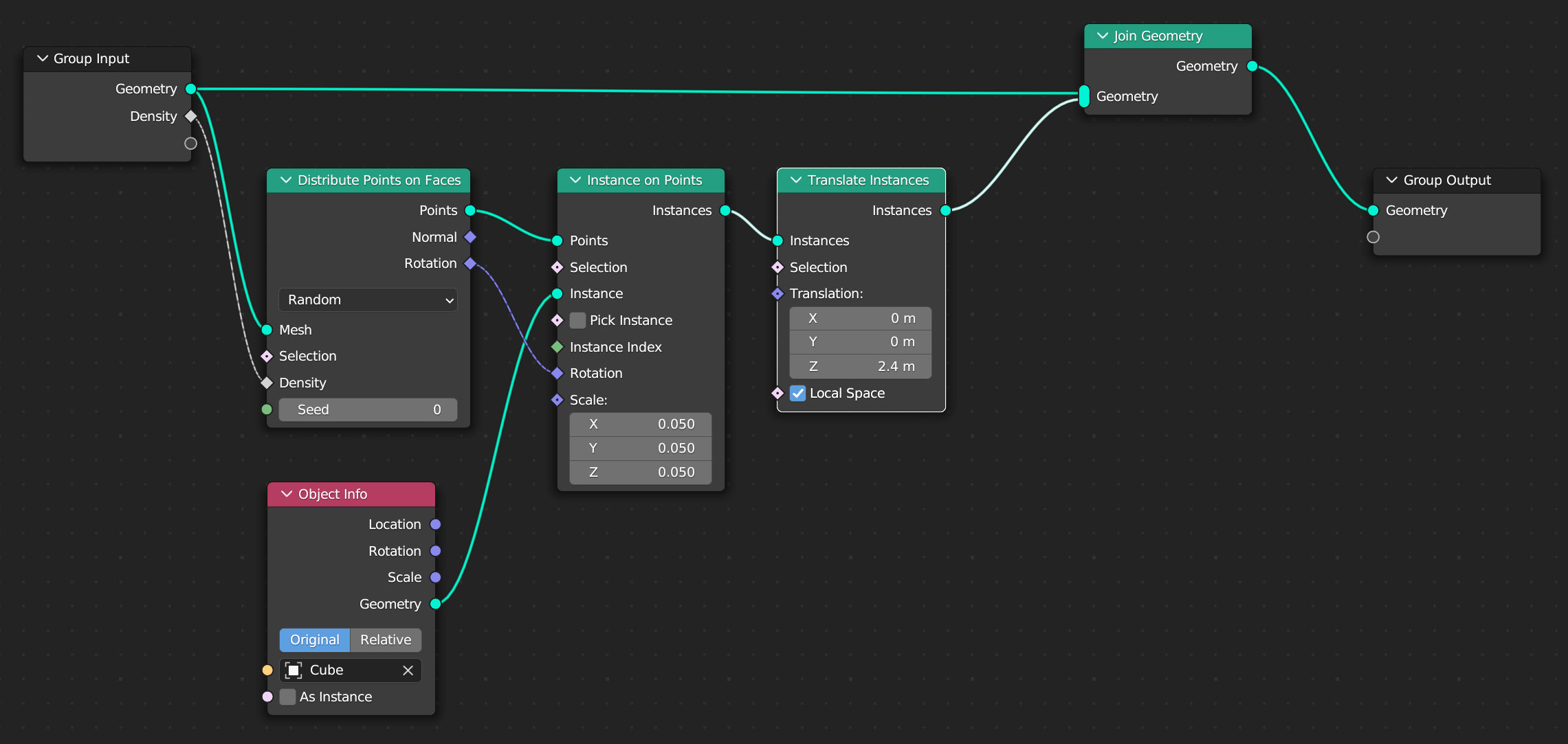
Proviamo ora a variare in modo casuale anche la posizione e le dimensioni dei cubi. Per le dimensioni il procedimento è identico a quello già visto poiché il nodo Instance on Points possiede un socket di input Scale oltre a quello Rotation (trascuriamo al momento il fatto che questi nodi siano a forma di rombo), anche se in questo caso potremo utilizzare un valore casuale non vettoriale, ma di tipo Float. Per effettuare delle traslazioni ricorreremo al nodo Translate Instances (famiglia Instances) togliendo la spunta alla casella Local Spaces come in figura.
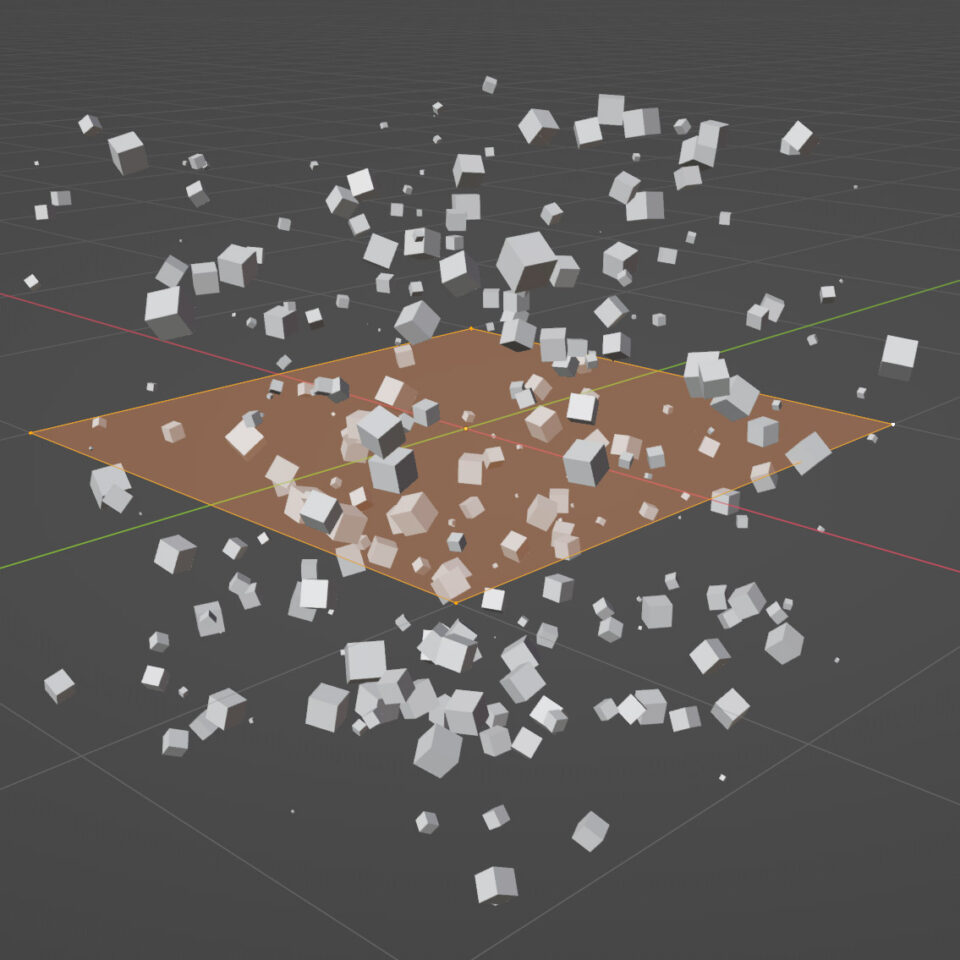
Quali osservazioni possiamo trarre dagli esempi appena visti e in particolar modo dall’ultimo? La prima è che con l’utilizzo di pochi nodi la banale geometria di partenza della mesh è stata completamente stravolta divenendo estremamente più complessa. La seconda e ultima osservazione riguarda l’uso del nodo Instance on Points. Il poter definire un insieme di punti nello spazio (siano questi i vertici di una mesh o una distribuzione di punti da essa derivata) al fine di duplicare e modificare un diverso modello (quello indicato in Object Info) rende di fatto il sistema dei geometry nodes alternativo ai sistemi particellari. Escludendo il caso della simulazione di erba o capelli, per i quali i particle systems offrono strumenti avanzati e ottimizzati a tal scopo, non conviene utilizzarli per lo scattering di qualsivoglia mesh su delle superfici 3D (pensate a dei sassi su un terreno piano) casi in cui ricorreremo ai geometry nodes. I sistemi particellari continuano a essere maggiormente indicati quando le particelle dovranno essere animate nel contesto di una simulazione fisica (capitolo 7). Vediamo dunque come realizzare lo scattering di uno o più oggetti su una superficie tramite il sistema dei geometry nodes. Nell’esempio utilizzeremo esclusivamente delle primitive elementari. In rete esistono dozzine di tutorial su centinaia sistemi di varia natura (dalle caramelle gelees a intere città procedurali) che utilizzano la seguente logica. Partiamo da una semplice sfera UV a cui applicheremo i seguenti nodi
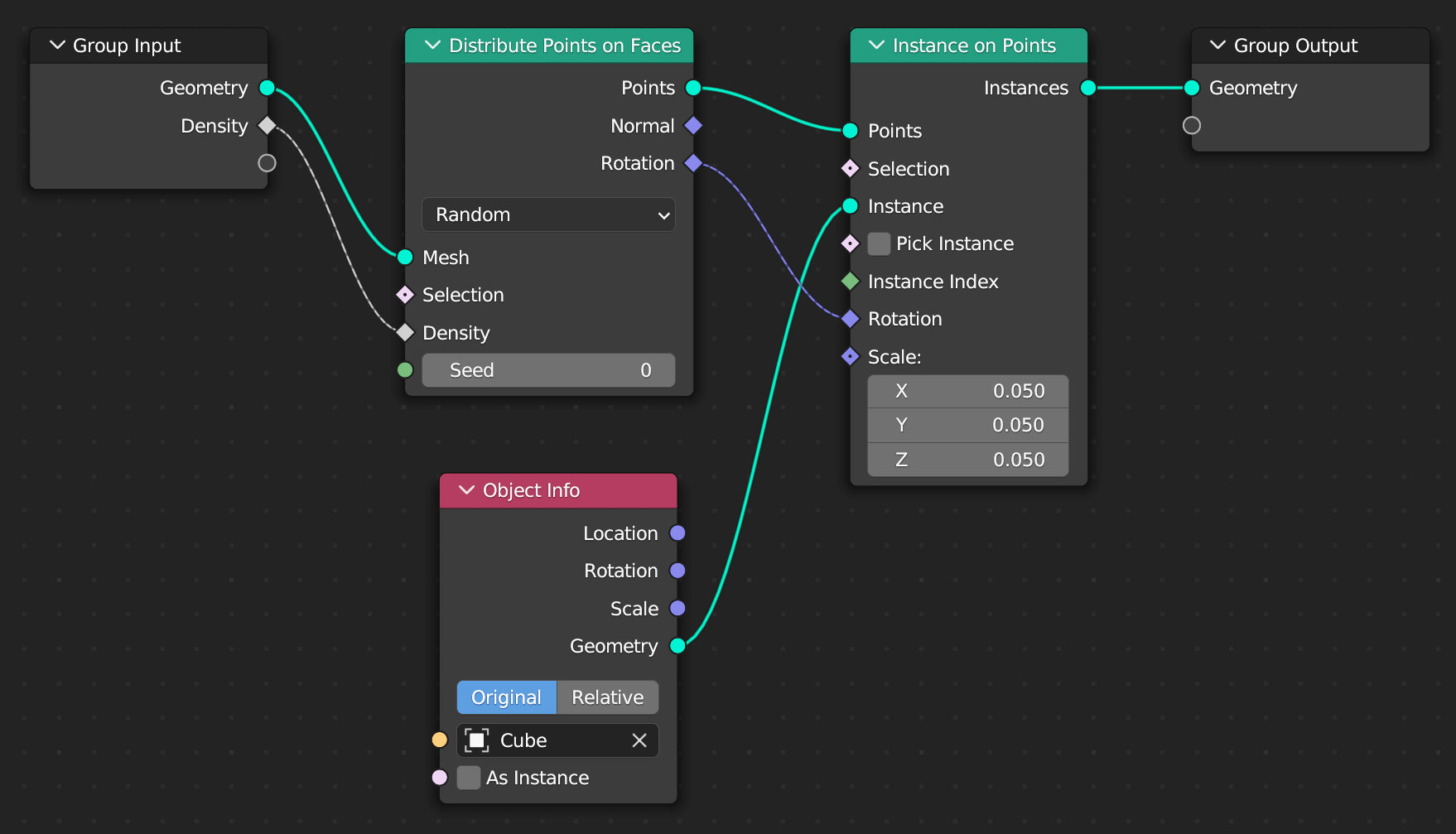
innanzitutto notiamo la presenza del nodo Distribute Points on Faces (famiglia point) il quale crea una distribuzione casuale di punti sulla superficie della mesh.

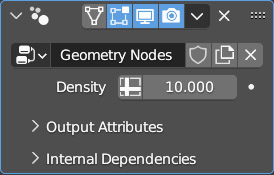
Questo nodo possiede il socket Density dove potremo variare la densità (e quindi il numero) di punti generati. Come vedete ho collegato questo valore al socket inizialmente vuoto del nodo Group Input. Il perché di questo collegamento lo scoprirete immediatamente andando a osservare il contesto properties Modifier, ovviamente relativo alla sfera, qui infatti compare una barra con cui è possibile modificare comodamente il parametro senza passare per forza dal node editor.
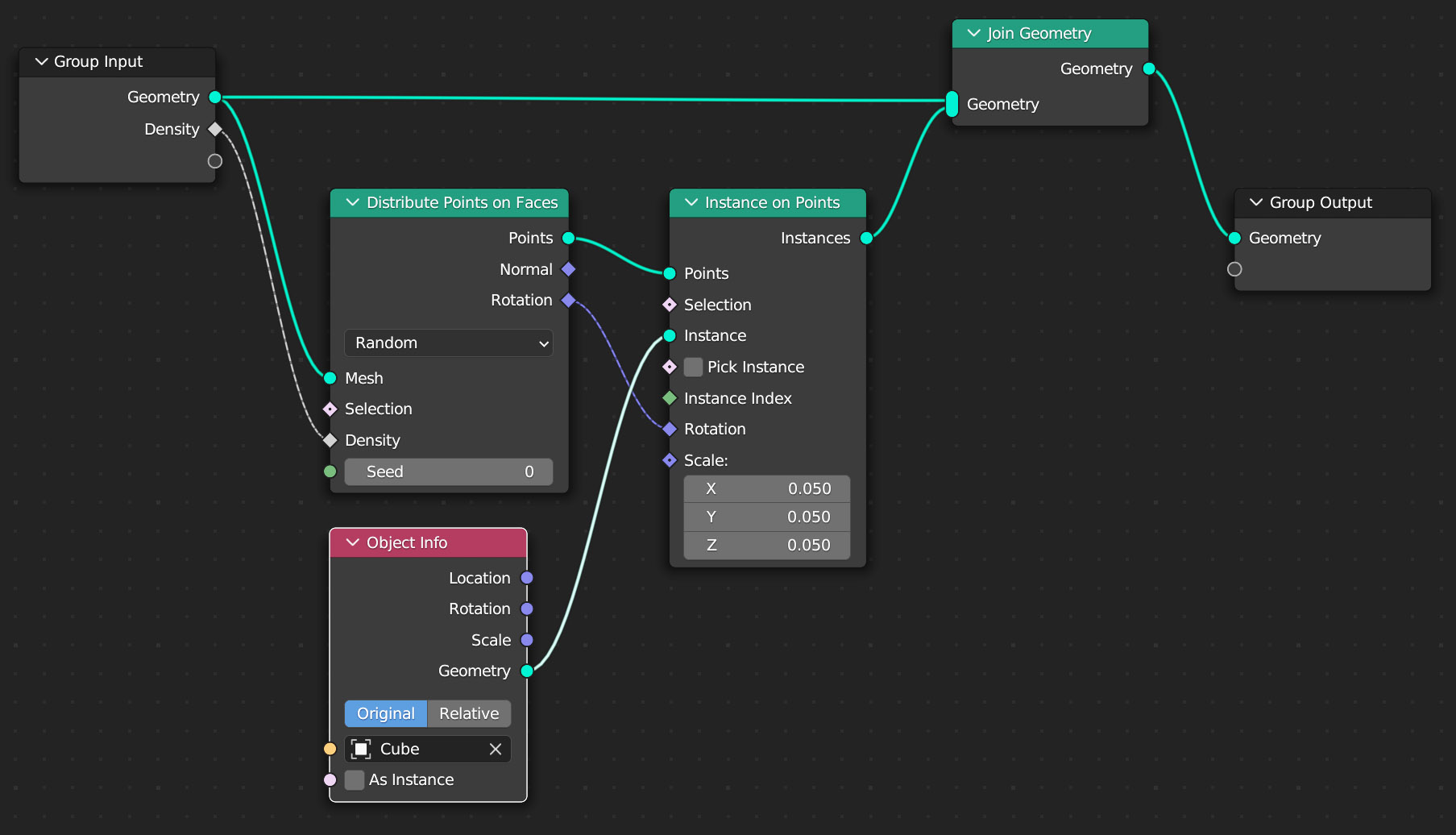
A questo punto proviamo a unire la distribuzione di cubi appena ottenuta alla superficie stessa da cui essi derivano. Potremo fare ciò con il nodo Join Geometry che consente di unire la superficie di partenza (tramite il socket geometry del nodo group input) a ciò che viene generato dalla restante catena di nodi tra loro connessi con i socket verdi

Questa è dunque la via per distribuire in modo casuale qualsiasi mesh sulla superficie di un altro modello. In questo esempio notiamo subito due cose. La prima è che i cubi risultano orientati e ruotati in modo coerente con la superficie generatrice, ossia secondo la direzione normale che passa per i punti generati in modo random sulla sfera. Questo è stato possibile collegando il socket di output Rotation del nodo Distribuite Points on Faces con l’omonimo socket di input del nodo Instances on Points. Successivamente vediamo che essendo i cubi distribuiti con il loro centro geometrico sui punti creati dal nodo Point Distribute, tali cubi andranno a intersecare la sfera. Per controllare la distanza dalla superficie, una distanza che ovviamente è da intendersi lungo la normale alla superficie stessa, basta inserire il nodo Translate Instances tra il nodo Instance on Points e Join Geometry, con la spunta attiva su Local Space e quindi variando a piacimento il valore Z.

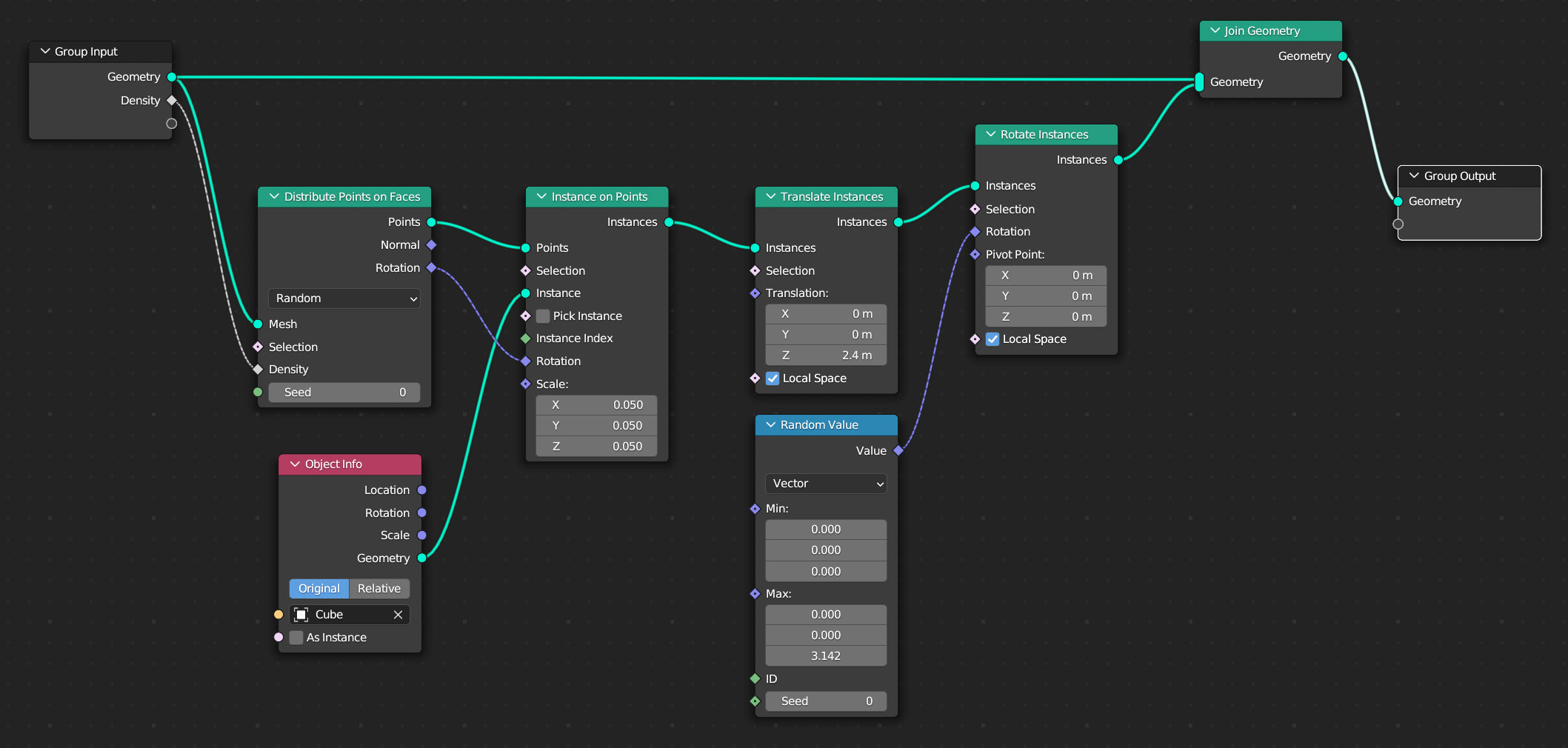
Proviamo infine ad aggiungere anche una rotazione uguale per tutti i cubi ovviamente lungo l’asse normale (immagine in alto). Essendo il socket di input Rotation del nodo Instance on Points già occupato, inseriamo il nodo Rotation Instances (local space attivo) tra i nodi Translate Instances e Join Geometry. A quel punto come al solito utilizziamo il nodo Random Value per rotazioni casuali.

Paragrafo successivo
Paragrafo precedente
Torna all’Indice
Nell’augurarti un divertente e produttivo studio di Blender, ti ricordo che puoi supportare questo progetto in due diversi modi: con una piccola donazione (paypal) oppure acquistando la versione PDF (su lulu.com) impaginata in modo professionale e ottimizzata per la visione su Tablet.